Picture a trapezoid. What comes to mind?
Does it look something like this?
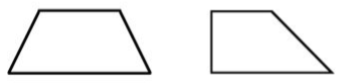
That’s what trapezoids looked like to me, anyway. My teacher told me trapezoids have a pair of parallel sides, and every picture I saw in my textbook looked like this. I never really had a reason to question it any further. But one day, I started thinking about it a little more.
After all, we know what this shape is:

A square, of course! But none of us would bat an eyelash if someone called it a rectangle, because it meets all the rules for rectangles. It just has a little something extra.
And speaking of rectangles:

There it is. Two pairs of parallel sides and all. But wait, that means it’s also a parallelogram!
And while we’re on the topic of parallelograms, there’s this little cutie:

Who doesn’t love a rhombus? Or is it a kite? Oh, it’s all three!
We have no trouble accepting these multiple classifications for different quadrilaterals. But suggest that a trapezoid can have at least one pair of parallel sides instead of exactly one pair, and everyone loses their minds!
In the summer of 2020, Zak Champagne and I discovered we were in opposite camps when it comes to the classification of trapezoids.
Well would you JUST LOOK at these LOVELY trapezoids! #cohort7 #mtholyokemath pic.twitter.com/u14J34saGT
— Shelby Strong 💗💜💙 (@Sneffleupagus) July 23, 2020
Trapezoids.
— Zak Champagne (@Zakchamp) August 22, 2020
No comment necessary from @Sneffleupagus pic.twitter.com/4EfO3mtS4F
Unbeknownst to me, I had wandered into a discussion that had been going on for some time: The Great Trapezoid Debate.
Camps had been established on opposing sides – those who defined trapezoids using an exclusive definition:
A trapezoid has exactly one pair of parallel sides
and those using an inclusive definition:
A trapezoid has at least one pair of parallel sides
Then came the ultimate blow.
Y'all. Why is he like this. 🤣🤣🤣 #cohort7 come look at this man. #MtHolyokeMath pic.twitter.com/4pTJJNbkSZ
— Shelby Strong 💗💜💙 (@Sneffleupagus) July 15, 2021
Since then, Berkeley Everett has stepped in to help us settle this debate once and for all. (Unless Zak wins, in which case the battle continues!)
Now, you might have reached this point and still not particularly have a firm opinion one way or another, and you wouldn’t be alone. And that’s totally okay! But I want to take a moment to talk about why (I think) this matters.
Math has a little bit of a reputation problem. It’s boring, it’s dry, there’s only one right answer or one right way of doing things. Everything is settled and nothing is up for debate. While the tides have started to turn a little bit, by and large this is still what comes to mind when most people think of math because this is what they experienced when they were in school.
Memorize this definition, use this algorithm, don’t ask questions.
The reality, however, is far more intriguing. Many of the things that we accept as fact in mathematics did not start out as universal truths. Equal signs, irrational numbers, negative numbers, even zero itself were up for debate until a collective agreement was reached, for one reason or another. Just recently, a fascinating conversation came up on Twitter about whether 0.999… is equal to one. I’m still not convinced that “convenience” is a good reason for zero to the power of zero to be equal to one instead of being undefined. But, I digress.
If we truly believe that our students are capable of being mathematicians and engaging with math authentically, then we also believe that they are capable of forming their own opinions and setting criteria that make sense to them and to others. Our job isn’t about building everything for students, but handing them the tools they need and offering guidance and encouragement. It’s about showing kids (and adults) that they, too, are able to examine evidence and come to a conclusion. It’s about demystifying a subject that has been exclusionary for far too long.
And that is why the Great Trapezoid Debate matters.
If you’re still having trouble choosing a side, Zak has written a post arguing for an exclusive argument on his blog. Check it out here and come tell us on Twitter whether you are #TeamInclusive or #TeamExclusive!
Note: Berkeley donates all of the proceeds from all shirt designs to TODOS, and through October 21, Zak will be donating an additional $5 for every Trapezoid shirt (or bag!) to The Trevor Project.

I am definitely on team “at least one pair” trapezoid group. My favorite activity in HS Geometry was to prove that all quadrilateral area formulas will work for a square of set length. It almost always ticked off half of my department when I displayed their work. If you believe that branches of the quadrilateral tree lead to a square, have heart. You are not alone!
Pingback: Can You Prime The Cube? | FiveThirtyEight
To be properly inclusive you should also include all triangles as trapeziums: They are trapeziums with one of the parallel sides reduced to zero length. But they still satisfy all the properties that other trapeziums have. The area formula “½(a+b)h” is true, even if one of a or b has zero length.
All trapeziums : ⏢ □ ▱ △ ▭
The only thing that will not pass is the word “Trapezoid” – That would mean “like a trapezium”, or “analogous to a trapezium”. Perhaps a 3D analogue, for example. The name of the same is “trapezium” and no colonial dialect can tell me otherwise.
I didn’t realize this was even a debate. Inclusive definitions are the norm in mathematics. Equilateral triangles are isosceles. Euclidean polygons are abstract polygons. Sums are integrals. Natural numbers are integers. And rectangles should be trapezoid.
We only really use exclusive definitions when there is an overriding reason to do so, like with the degree of a polynomial (lines are not parabolas), or the rank of a set (the empty set is not rank 1). I think there is a good reason to argue that triangles are not trapezoids but triangular numbers are trapezoidal numbers. But arguing that parallelograms are NOT trapezoids? That seems like a weird one, a sort of arbitrary exclusion like saying that circles are not ellipses or piecewise-straight graphs are not curves. Are there any real arguments to support this exclusive definition?
that trapizoid is sooo cute.
Right?? So cute, but so sad. They just want to be part of the club!